Aprendizaje Profundo

En los últimos años, ha habido un resurgimiento en el campo de la Inteligencia Artificial. Se ha extendido más allá del mundo académico, con grandes figuras como Google, Microsoft y Facebook, quienes han creado sus propios equipos de investigación, obteniendo impresionantes adquisiciones.

Se comenta que esto puede atribuirse a la gran cantidad de datos brutos generados por los usuarios de redes sociales, muchos de los cuales deben ser analizados, al igual que al poder computacional precario disponible a través de GPGPUs.

Pero más allá de estos fenómenos, este resurgimiento se ha impulsado en gran parte por una nueva tendencia en la IA, concretamente en el aprendizaje de máquina, conocida como “aprendizaje profundo”. En este tutorial, te voy a presentar los conceptos claves y algoritmos detrás del aprendizaje profundo, empezando por la unidad más simple de la composición hasta llegar a los conceptos de aprendizaje automático en Java.

(Para una descripción completa: Soy también el autor de una biblioteca de aprendizaje profundo de Java, disponible aquí, y los ejemplos de este artículo se implementan utilizando la biblioteca de arriba Si te gusta, puedes apoyarla dándole una estrella en GitHub, por lo cual estaría muy agradecido. Las instrucciones de uso están disponibles en la página de inicio.)

Un Tutorial de Treinta Segundos sobre Aprendizaje de Máquinas

En caso de que no estés familiarizado, echa un vistazo a esta introducción al aprendizaje de máquinas:

El procedimiento general es el siguiente:

1. Tenemos un algoritmo al que se le da un puñado de ejemplos etiquetados; por ejemplo, 10 imágenes de perros con la etiqueta 1 (“perro”) y 10 imágenes de otras cosas con la etiqueta 0 (“No perro”) - Ten en cuenta que estamos usando principalmente para este post, clasificación supervisada y binaria.
2. El algoritmo “aprende” a identificar imágenes de perros y cuando se le alimenta con una nueva imagen, espera producir la etiqueta correcta (1 si se trata de una imagen de un perro, y 0 en caso contrario).

Esta configuración es muy general: los datos podrían ser síntomas y enfermedades de las etiquetas, o tus datos podrían ser imágenes de personajes escritos a mano y las etiquetas los personajes que representan.

Perceptrones: Aprendizaje Profundo de Algoritmos

Uno de los primeros algoritmos de entrenamiento supervisado es el perceptrón; un bloque de construcción básico de redes neuronales.

Supongamos que tenemos puntos n en el plano, con la etiqueta ‘0’ y ‘1’. Nos dan un nuevo punto y queremos adivinar su etiqueta (esto es similar al escenario “perro” y “No perro” de arriba). ¿Cómo lo hacemos?

Un buen acercamiento podría ser mirar al vecino más cercano y devolver la etiqueta desde ese punto. Pero una manera un poco más inteligente de hacer las cosas, sería elegir una línea que separe mejor los datos etiquetados y usar eso como clasificador.

En este caso, cada pieza de datos de entrada se representa como un vector x = ( x_1, x_2 ) y nuestra función sería algo así como “ ‘0’ si está por debajo de la línea, ‘1’ si está por encima”.

Para representar esto matemáticamente, deja que nuestro separador sea definido por un vector de pesos w y un desplazamiento vertical sesgo b. Entonces, nuestra función combinaría las entradas y los pesos con una función de transferencia de suma ponderada:

El resultado de esta función de transferencia sería entonces alimentada a una función de activación para producir un etiquetado. En el ejemplo anterior, nuestra función de activación era un umbral de corte (por ejemplo, 1 si es mayor que un cierto valor):

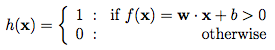
Entrenando el Perceptrón

El entrenamiento del perceptrón consiste en alimentarlo con múltiples muestras de entrenamiento y el cálculo de la salida para cada uno de ellos. Después de cada muestra, los pesos w se ajustan de tal manera a fin de minimizar el error de salida, definido como la diferencia entre la salida deseada (objetivo) y la real. Hay otras funciones de error, como el error cuadrado medio, pero el principio básico de entrenamiento sigue siendo el mismo.

Inconvenientes del Perceptrón Simple

El enfoque del perceptrón simple para el aprendizaje profundo, tiene un gran inconveniente: sólo puede aprender funciones linealmente separables. ¿Qué tan importante es este inconveniente? Toma XOR, una función relativamente simple, y notarás que no puede ser clasificada por un separador lineal (nota el intento fallido, a continuación):

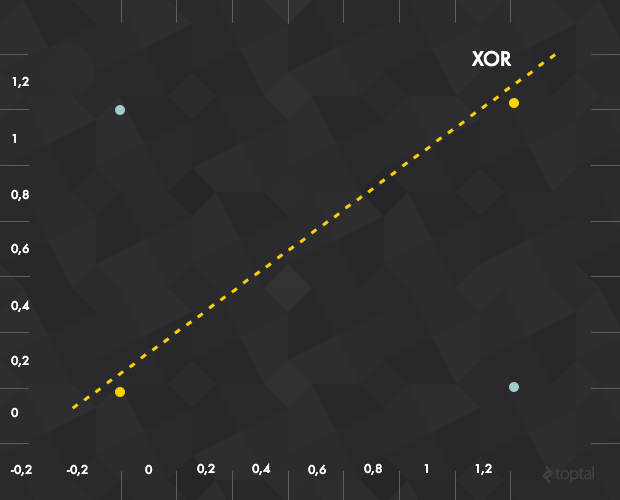
Para hacer frente a este problema, tendremos que utilizar un perceptrón multicapa, también conocido como red neuronal feedforward: en efecto, vamos a componer una gran cantidad de estos perceptrones para crear un mecanismo más potente para el aprendizaje.

Redes Neuronales Feedforward para el Aprendizaje Profundo

Una red neuronal es en realidad una composición de perceptrones conectados de diferentes maneras, y que operan con diferentes funciones de activación.

Para empezar, vamos a ver la red neuronal feedforward, que tiene las siguientes propiedades:

• Una entrada, salida, y una o más capas ocultas. La figura anterior muestra una red con una capa de entrada de 3 unidades, 4-unidades de capa oculta y una capa de salida con 2 unidades (los términos unidades y neuronas son intercambiables).
• Cada unidad es un perceptrón simple, como el descrito anteriormente.
• Las unidades de la capa de entrada sirven como entradas para las unidades de la capa oculta, mientras que las unidades de la capa oculta son entradas para la capa de salida.
• Cada conexión entre dos neuronas tiene un peso w (similar a los pesos perceptron).
• Cada unidad de la capa t suele estar conectada a cada unidad de la capa t anterior - 1 (aunque se podrían desconectar mediante el establecimiento de su peso a 0).
• Para procesar los datos de entrada, sujetas el vector de entrada a la capa de entrada, estableciendo los valores del vector como “salidas” para cada una de las unidades de entrada. En este caso en particular, la red puede procesar un vector de entrada tridimensional (debido a las 3 unidades de entrada). Por ejemplo, si tu vector de entrada es [7, 1, 2], entonces ajustarías la salida de la unidad de entrada superior, a 7, la unidad del medio a 1, y así sucesivamente. Estos valores se propagan hacia adelante hasta las unidades ocultas, utilizando la función de transferencia suma ponderada para cada unidad oculta (de ahí el término propagación hacia adelante), que a su vez calcula sus salidas (función de activación).
• La capa de salida calcula sus salidas de la misma forma que la capa oculta. El resultado de la capa de salida es la salida de la red.

Más Allá de la Linealidad

¿Qué pasa si sólo se permite a cada uno de nuestros perceptrones utilizar una función de activación lineal? Entonces, la salida final de nuestra red será aún una función lineal de las entradas, simplemente ajustada con una tonelada de diferentes pesos que se recogió a través de la red. En otras palabras, una composición lineal de un grupo de funciones lineales todavía es sólo una función lineal. Si nos limitamos a las funciones de activación lineales, entonces la red neuronal feedforward no es más poderosa que el perceptrón, sin importar cuántas capas tenga.

Una composición lineal de un montón de funciones lineales sigue siendo sólo una función lineal, por lo que la mayor parte de las redes neuronales utilizan funciones de activación no lineales.

Debido a esto, la mayoría de las redes neuronales usan funciones de activación no lineales como logistic, tanh, binary or rectifier. Sin ellos, la red sólo puede aprender las funciones que son combinaciones lineales de sus entradas.

Entrenando Perceptrones

El algoritmo de aprendizaje profundo más común para entrenamiento supervisado de los perceptrones multicapa se conoce como propagación reversa. El procedimiento básico:

1. Una muestra de entrenamiento se presenta y se propaga hacia adelante a través de la red.
2. Se calcula el error de salida, por lo general el error cuadrático medio:
   
   Donde t es el valor objetivo e y es la salida real de la red. Otros cálculos de error también son aceptables, pero el MSE es una buena opción.
3. Los errores de red se reducen usando un método llamado descenso de gradiente estocástico.
   El descenso gradiente es universal, pero en el caso de redes neuronales, esto sería un gráfico del error de entrenamiento como una función de los parámetros de entrada. El valor óptimo para cada peso es aquel en que el error alcanza un mínimo global. Durante la fase de entrenamiento, los pesos se actualizan en pequeños pasos (después de cada muestra de entrenamiento o un mini-grupo de varias muestras) de manera que siempre están tratando de alcanzar el mínimo global, pero esto no es una tarea fácil, ya que a menudo terminan en mínimos locales, como el que se ve en la derecha. Por ejemplo, si el peso tiene un valor de 0,6, se debe cambiar a 0,4.
   Esta cifra representa el caso más simple, aquella en la que el error depende de un solo parámetro. Sin embargo, el error de red depende de cada peso de red y la función de error es mucho, mucho más compleja.
   Afortunadamente, la propagación hacia atrás proporciona un método para la actualización de cada peso entre dos neuronas, con respecto al error de salida. La derivación en sí es bastante complicada, pero la actualización de peso para un determinado nodo tiene la siguiente forma (simple):
   

Donde E es el error de salida, y w_i es el peso de la entrada i a la neurona.

En esencia, el objetivo es moverse en la dirección de la gradiente con respecto al peso i. El término clave es, por supuesto, la derivada del error, lo cual no siempre es fácil de calcular: ¿cómo encontrar este derivado para un peso al azar de un nodo oculto al azar en medio de una gran red?

La respuesta: a través de propagación hacia atrás. Los errores se calculan en primer lugar en las unidades de salida, donde la fórmula es bastante simple (basado en la diferencia entre el objetivo y los valores predeterminados), y luego se propagan a través de la red de una manera inteligente, permitiéndonos actualizar de manera eficiente nuestros pesos durante el entrenamiento y (con suerte) llegar a un mínimo.

Capa Oculta

La capa oculta es de particular interés. Por el teorema de aproximación universal, una única red de capa oculta con un número finito de neuronas puede ser entrenada para la aproximación de una función arbitraria al azar. En otras palabras, una sola capa oculta es lo suficientemente potente como para aprender cualquier función. Dicho esto, a menudo aprendemos mejor en la práctica con múltiples capas ocultas (es decir, redes más profundas).

La capa oculta es donde la red guarda la representación abstracta interna de los datos de entrenamiento.

La capa oculta es donde la red guarda la representación abstracta interna de los datos de entrenamiento, similar a la forma en que un cerebro humano (analogía muy simplificada) tiene una representación interna del mundo real. En adelante en el tutorial, vamos a ver diferentes formas de jugar un poco con la capa oculta.

Un Ejemplo de Red

Se puede ver una red simple (4-2-3 capa) de feedforward neural que clasifica el conjunto de datos IRIS, implementado en Java aquí, a través del método testMLPSigmoidBP. El conjunto de datos contiene tres clases de plantas de iris con características como la longitud sépalo, longitud pétalo, etc. Se proporciona a la red 50 muestras por clase. Las características se sujetan a las unidades de entrada, mientras que cada unidad de salida corresponde a una única clase del conjunto de datos: “1/0/0” indica que la planta es de clase Setosa, “0/1/0” indica versicolor, y “0/0/1” indica Virginica. El error de clasificación es 2/150 (es decir, no clasifica correctamente 2 muestras de 150).

El Problema con las Grandes Redes

Una red neuronal puede tener más de una capa oculta: en ese caso, las capas superiores están “construyendo” nuevas abstracciones en la parte superior de las capas anteriores. Y como hemos mencionado antes, a menudo se puede aprender mejor en la práctica con las redes más grandes.

Sin embargo, el aumento del número de capas ocultas conduce a dos problemas conocidos:

1. Desaparición del Gradiente: a medida que añadimos más y más capas ocultas, la propagación hacia atrás se vuelve cada vez menos útil en la transmisión de información a las capas inferiores. En efecto, como la información se pasa de nuevo, los gradientes comienzan a desaparecer y se hacen más pequeños en relación con los pesos de las redes.
2. Sobreajuste: tal vez éste sea el problema central en el aprendizaje automático. En pocas palabras, el sobreajuste describe el fenómeno de ajuste de los datos de entrenamiento demasiado cerca, tal vez con la hipótesis de que son muy complejos. En tal caso, el alumno termina el montaje de los datos de entrenamiento muy bien pero se desarrollará muy mal en ejemplos reales.

Veamos algunos algoritmos de aprendizaje profundo para abordar estas cuestiones.

Autoencoders

La mayoría de las clases introductorias de aprendizaje automático tienden a terminar con las redes neuronales feedforward. Pero el espacio de posibles redes es mucho más rico, así que continuemos.

Un autoencoder es típicamente una red neuronal feedforward, que tiene como objetivo aprender una representación (codificación) comprimida y distribuida de un conjunto de datos.

Conceptualmente, la red está capacitada para “recrear” la entrada, es decir, la entrada y los datos de objetivo son los mismos. En otras palabras: estás tratando de usar lo mismo como salida y entrada, pero comprimido de alguna manera. Este es un enfoque confuso, así que vamos a ver un ejemplo.

Compresión de la Entrada: Las Imágenes en Escala de Grises

Digamos que los datos de entrenamiento constan de imágenes en escala de grises de 28x28 y el valor de cada pixel se fija a una neurona de capa de entrada (es decir, la capa de entrada tendrá 784 neuronas). Luego, la capa de salida tendría el mismo número de unidades (784) como la capa de entrada y el valor objetivo para cada unidad de salida, sería el valor de escala de grises de un pixel de la imagen.

La intuición detrás de esta arquitectura es que la red no va a aprender un “mapeo” entre los datos de entrenamiento y sus etiquetas, pero si aprenderá la estructura interna y las características de los propios datos. (Debido a esto, la capa oculta también se denomina detector de característica.) Por lo general, el número de unidades ocultas es más pequeño que las capas de entrada / salida, lo que obliga a la red a aprender solamente las características más importantes y logra una reducción de dimensionalidad.

Queremos unos pequeños nodos en el medio para aprender los datos a nivel conceptual, produciendo una representación compacta.

En efecto, queremos unos pequeños nodos en el medio para aprender realmente los datos a nivel conceptual, produciendo una representación compacta que de alguna manera capte las características fundamentales de nuestra entrada.

La Enfermedad de la Gripe

Para demostrar aún más autoencoders, vamos a ver una aplicación más. En este caso, vamos a utilizar un conjunto de datos simple, que consiste en síntomas de la gripe (crédito a esta entrada en el blog de la idea). Si estás interesado, el código para este ejemplo se puede encontrar en el método testAEBackpropagation.

He aquí cómo el conjunto de datos se desglosa:

• Hay seis entidades de entrada binarias.
• Los tres primeros son los síntomas de la enfermedad. Por ejemplo, 1 0 0 0 0 0 indica que este paciente tiene temperatura alta, mientras que 0 1 0 0 0 0 indica tos, 1 1 0 0 0 0 indica la tos y alta temperatura, etc.
• Las tres últimas características son síntomas “de venta libre”; cuando un paciente tiene uno de estos, es menos probable que él o ella esté enfermo/a. Por ejemplo, 0 0 0 1 0 0 indica que este paciente tiene una vacuna contra la gripe. Es posible tener combinaciones de los dos conjuntos de características: 0 1 0 1 0 0 indica un paciente vacunado con tos, y así sucesivamente.

Vamos a considerar que un paciente está enfermo. Cuando él o ella tiene al menos dos de las tres primeras características, y saludable si él o ella tiene al menos dos de las tres últimas (con desempates que se rompen a favor de los pacientes sanos), por ejemplo:

• 111000, 101000, 110000, 011000, 011100 = enferma
• 000111, 001110, 000101, 000011, 000110 = sano

Vamos a entrenar a un autoencoder (mediante propagación hacia atrás) con seis unidades de entrada y seis de salida, pero sólo dos unidades ocultas.

Después de varios cientos de iteraciones, se observa que cuando cada una de las muestras de “enfermos” se presentan a la red de aprendizaje de máquina, una de las dos unidades ocultas (la misma unidad para cada muestra “enfermo”) siempre exhibe un valor de activación más alto que la otra. Por el contrario, cuando se presenta una muestra “sano”, la otra unidad oculta tiene una mayor activación.

De Vuelta al Aprendizaje de Máquina

En esencia, nuestras dos unidades ocultas han aprendido una representación compacta del conjunto de datos de los síntomas de la gripe. Para ver cómo esto se relaciona con el aprendizaje, volvemos al problema de sobreajuste. Mediante el entrenamiento de nuestra red para aprender una representación compacta de los datos, estamos dando preferencia a una representación más simple en lugar de una hipótesis altamente compleja que sobre-ajusta los datos de entrenamiento.

En cierto modo, al favorecer estas representaciones más simples, estamos tratando de aprender los datos en un sentido más verdadero.

• 
• 
• Máquina de Boltzmann Restringidas

El siguiente paso lógico es mirar las máquinas de Boltzmann restringidas (MBR), una red neuronal generativa que puede aprender una distribución de probabilidad sobre su propio conjunto de entradas.

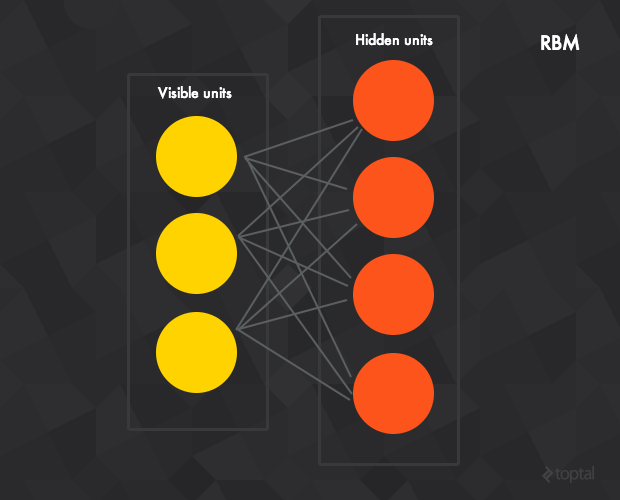
Dichos mecanismos están compuestos de una capa de sesgo (bias) oculta y visible. A diferencia de las redes feedforward, las conexiones entre las capas visibles y ocultas son no-dirigidas (los valores se pueden propagar tanto en direcciones visible-a-oculto y oculto-a-visible) y completamente conectadas (cada unidad de una capa está conectada a cada unidad en la siguiente capa, si permitimos que cualquier unidad en cualquier capa se conecte a cualquier otra capa, entonces tendríamos un Boltzmann (en lugar de una máquina de Boltzmann restringida).

El estándar MBR tiene binario oculto y unidades visibles: es decir, la activación de la unidad es 0 o 1 bajo una distribución de Bernoulli, pero hay variantes con otras no-linealidades.

Mientras que los investigadores han tenido conocimiento sobre las MBR desde hace algún tiempo, la reciente introducción del algoritmo de entrenamiento no supervisado de la divergencia contrastiva, ha renovado el interés.

La Divergencia Contrastiva

El algoritmo de un solo paso de la divergencia contrastiva (CD-1) funciona así:

1. Fase positiva:
   • Una muestra de entrada v se sujeta a la capa de entrada.
   • v se propaga a la capa oculta de una manera similar como a las redes feedforward. El resultado de las activaciones de la capa oculta es h.
2. Fase negativa:
   • Propagar h de regreso a la capa visible con resultado v’ (las conexiones entre las capas visibles y ocultas son no-dirigidas y por lo tanto permiten el movimiento en ambas direcciones).
   • Propagar la nueva v’ de vuelta a la capa oculta con resultado de activaciones h’.
3. Actualización de peso:
   
   Donde a es la tasa de aprendizaje y v, v’, h, h’, y w son vectores.

La intuición detrás del algoritmo es que la fase positiva (h dada v) refleja la representación interna de la red de datos de la vida real. Mientras tanto, la fase negativa representa un intento de recrear los datos, basados en esta representación interna (v’ dada h). El objetivo principal es que los datos generados sean lo más cercano posible a la de la vida real y esto se refleja en la fórmula actualización peso.

En otras palabras, la red tiene una percepción de cómo los datos de entrada pueden ser representados, por lo que trata de reproducir los datos basándose en esta percepción. Si su reproducción no es lo suficientemente cercana a la realidad, hace un ajuste y lo intenta de nuevo.

Volviendo a la Gripe

Para demostrar la divergencia contrastiva, usaremos el mismo conjunto de datos de síntomas que utilizamos anteriormente. La red de prueba es una MBR con seis unidades visibles y dos unidades ocultas. Vamos a entrenar la red, utilizando la divergencia contrastiva con los síntomas v sujetos a la capa visible. Durante las pruebas, los síntomas se presentan de nuevo a la capa visible; luego los datos se propagan a la capa oculta. Las unidades ocultas representan el estado enfermo / sano, una arquitectura muy similar a la autoencoder (propagación de datos de la capa visible a la oculta).

Después de varios cientos de iteraciones, se observa el mismo resultado que con autoencoders: una de las unidades ocultas tiene un valor mayor de activación cuando se presenta alguna de las muestras de “enfermos”, mientras que el otro está siempre más activo para las muestras de “sanos”.

Puedes ver este ejemplo en acción en el método testContrastiveDivergence.

Redes Profundas

Hemos demostrado ahora que las capas ocultas de autoencoders y las MBR actúan como detectores de características eficaces; pero es raro que podamos utilizar estas funciones directamente. De hecho, el conjunto de datos anterior, es más una excepción que una regla. En su lugar, tenemos que encontrar la manera de utilizar estas características detectadas, indirectamente.

Por suerte, se descubrió que estas estructuras pueden ser apiladas para formar redes profundas. Estas redes pueden ser entrenadas codiciosamente, una capa a la vez, para ayudar a superar la desaparición de gradientes y problemas de sobreajuste asociados con la clásica propagación hacia atrás.

Las estructuras resultantes son a menudo bastante potentes, produciendo resultados impresionantes. Tomemos, por ejemplo, la famosa “cat” paper de Google, en el que utilizan una clase especial de autoencoders profundos para “aprender” la detección del rostro humano y de gatos, basado en datos no marcados.

Miremos más de cerca.

Autoencoders Apilados

Como su nombre lo indica, esta red consiste en múltiples autoencoders apilados.

La capa oculta de autoencoder t actúa como una capa de entrada a autoencoder t + 1. La capa de entrada del primer autoencoder es la capa de entrada para toda la red. El procedimiento de entrenamiento de greedy layer-wise funciona así:

1. Entrena al primer autoencoder (t=1, o las conexiones de color rojo en la figura anterior, pero con una capa de salida adicional) de forma individual utilizando el método de propagación hacia atrás con todos los datos de entrenamiento disponibles.
2. Entrena al segundo autoencoder t=2 (conexiones verdes). Dado que la capa de entrada para t=2 es la capa oculta de t=1, ya no estamos interesados en la capa de salida de t=1 y la quitamos de la red. El entrenamiento comienza sujetando una muestra de entrada a la capa de entrada de t=1, que se propaga hacia adelante a la capa de salida de t=2. A continuación, los pesos (entrada-oculta y oculta-salida) de t=2 se actualizan mediante propagación hacia atrás. t=2 utiliza todas las muestras de entrenamiento, similar a t=1.
3. Repite el procedimiento anterior para todas las capas (es decir, elimina la capa de salida del autoencoder anterior, sustitúyela por otra autoencoder, y entrénala con propagación hacia atrás).
4. Pasos 1-3 se llaman pre-entrenamiento y dejan los pesos inicializados correctamente. Sin embargo, no hay mapeo entre los datos de entrada y las etiquetas de salida. Por ejemplo, si la red está entrenada para reconocer imágenes de dígitos escritos a mano, todavía no es posible mapear las unidades del último detector de características (es decir, la capa oculta del último autoencoder) al tipo de dígitos de la imagen. En ese caso, la solución más común es añadir una o más capas enteramente conectadas con la última capa (conexiones azules). Toda la red ahora se puede ver como un perceptrón de múltiples capas y es entrenado utilizando propagación hacia atrás (este paso también se denomina ajuste fino).

Entonces, los autoencoders apilados tratan de proporcionar un método de pre-entrenamiento eficaz para inicializar los pesos de una red, dejándote con un complejo perceptrón multicapa, que está listo para entrenar (o hacer ajuste fino).

Las Redes de Creencias Profundas

Al igual que con autoencoders, también podemos apilar máquinas de Boltzmann, para crear una clase conocida como redes de creencias profundas (DBN).

En este caso, la capa oculta de la MBR t actúa como una capa visible de MBR t + 1. La capa de entrada de la primera MBR es la capa de entrada para toda la red, y la greedy layer-wise de pre-entrenamiento funciona así:

1. Capacita la primera MBR t=1, utilizando divergencia contrastiva con todas las muestras de entrenamiento.
2. Capacita la segunda MBR t=2. Puesto que la capa visible para t=2 es la capa oculta de t=1, la formación comienza por sujetar la muestra de entrada a la capa visible de t=1, la cual se propaga hacia adelante a la capa oculta de t=1. Estos datos sirven, posteriormente, para iniciar el entrenamiento de divergencia contrastiva para t=2.
3. Repite el procedimiento anterior para todas las capas.
4. Al igual que en los autoencoders apiladas, después de pre-entrenar, la red se puede ampliar mediante la conexión de una o más capas completamente conectadas a la capa oculta final MBR. Esto forma un perceptrón de múltiples capas que puede ser afinado mediante propagación hacia atrás.

Este procedimiento es similar al de autoencoders apilados, pero con los autoencoders siendo reemplazados por MBR, y la propagación hacia atrás es reemplazada con el algoritmo de divergencia contrastiva.

(Nota: para más información sobre la construcción y entrenamiento de autoencoders apilados o redes de creencias profundas, visita el código de ejemplo aquí.)

Redes Convolucionales

Como arquitectura final de aprendizaje profundo, vamos a echar un vistazo a las redes convolucionales, una clase particularmente interesante y especial de las redes feedforward, que están muy bien adaptadas al reconocimiento de imágenes.

Antes de examinar la estructura real de las redes convolucionales, en primer lugar definiremos un filtro de imagen o una región cuadrada con pesos asociados. Un filtro se aplica a través de una imagen de entrada completa, y a menudo aplicarás varios filtros. Por ejemplo, podrías aplicar cuatro filtros de 6x6 a una imagen de entrada dada. Luego, el píxel de salida con coordenadas 1,1 es la suma ponderada de un cuadrado de 6x6 píxeles de entrada, con la esquina superior izquierda de 1,1 y los pesos del filtro (que también es un cuadrado 6x6). Pixel de salida de 2,1 es el resultado del cuadrado de entrada, con la esquina superior izquierda de 2,1 y así sucesivamente.

Con esto revisado, estas redes se definen por las siguientes propiedades:

• Las capas convolucionales aplican una serie de filtros a la entrada. Por ejemplo, la primera capa de convolución de la imagen podría tener cuatro filtros de 6x6. El resultado de un filtro aplicado a través de la imagen, se denomina mapa de características (FM) y la cantidad de mapas de función es igual al número de filtros. Si la capa anterior también es convolucional, los filtros se aplican en todas las FM con diferentes pesos, por lo que cada FM de entrada está conectado a cada FM de salida. La intuición detrás de los pesos compartidos a través de la imagen es que, se detectarán las características independientemente de su ubicación, mientras que la multiplicidad de filtros permite a cada uno de ellos detectar un conjunto diferente de características.
• Las capas submuestreo reducen el tamaño de la entrada. Por ejemplo, si la entrada consiste de una imagen 32x32, y la capa tiene una región de submuestreo de 2x2, el valor de salida sería una imagen de 16x16, lo que significa que 4 pixeles (cada cuadrado de 2x2) de la imagen de entrada se combinan en un píxel de una sola salida. Existen múltiples maneras de submuestra, pero los más populares son el pooling máximo, pooling promedio, y pooling estocástico.
• La última capa de submuestreo (o convolucional) suele estar relacionada con una o más capas totalmente conectadas, la última de las cuales representa los datos de objetivo.
• El entrenamiento se realiza usando propagación hacia atrás modificada, la cual toma en cuenta las capas de submuestreo y actualiza los pesos de filtro convolucional, basándose en todos los valores a los que se aplica dicho filtro.

Se pueden ver varios ejemplos de redes convolucionales entrenadas (con propagación hacia atrás) en el conjunto de datos MNIST (imágenes en escala de grises de cartas escritas a mano) aquí, específicamente en los métodos testLeNet* (recomendaría testLeNetTiny2, ya que logra una baja tasa de error de alrededor del 2% en un período de tiempo relativamente corto). También hay una agradable visualización JavaScript de una red similar aquí.

Implementación

Ahora que hemos revisado las variantes de la red neural más comunes, me gustaría escribir un poco sobre los desafíos planteados durante la ejecución de estas estructuras profundas de aprendizaje.

En términos generales, mi objetivo en la creación de una biblioteca de aprendizaje profundo era (y sigue siendo) construir un marco basado en una red neuronal, que cumpliera con los siguientes criterios:

• Una arquitectura común capaz de representar diversos modelos (todas las variantes en las redes neuronales que hemos visto anteriormente, por ejemplo).
• La capacidad de utilizar diversos algoritmos de entrenamiento (de propagación hacia atrás, divergencia contrastiva, etc.).
• Rendimiento decente.

Para satisfacer estos requisitos, tomé un enfoque escalonado (o modular) para el diseño de software.

Estructura

Empecemos con lo básico:

• NeuralNetworkImpl es la clase base para todos los modelos de redes neuronales.
• Cada red contiene un conjunto de capas.
• Cada capa tiene una lista de conexiones, donde una conexión es una relación entre dos capas, de tal manera que la red es un gráfico acíclico dirigido.

Esta estructura es lo suficientemente ágil para ser utilizada para las clásicas redes feedforward, así como para MBR y arquitecturas más complejas como ImageNet.

También permite que una capa sea parte de más de una red. Por ejemplo, las capas en una red de creencia profunda también son capas en sus correspondientes MBR.

Además, esta arquitectura permite a un DBN ser visto como una lista de MBR apilados durante la fase de pre-entrenamiento, y como una red feedforward durante la fase de ajuste fino, que es intuitivamente agradable, al igual que programáticamente conveniente.

Propagación de Datos

El siguiente módulo se encarga de la propagación de datos a través de la red, un proceso de dos pasos:

1. Determina el orden de las capas. Por ejemplo, para conseguir los resultados de un perceptrón de múltiples capas, los datos son “sujetados” a la capa de entrada (por lo tanto, esta es la primera capa que se calcula) y propagados hasta el final a la capa de salida. Para actualizar los pesos durante la propagación hacia atrás, el error de salida tiene que ser propagado a través de cada capa en orden de anchura, a partir de la capa de salida. Esto se consigue utilizando diferentes implementaciones de LayerOrderStrategy, que se aprovecha de la estructura gráfica de la red, empleando diferentes métodos de gráfico de recorrido. Algunos ejemplos incluyen la estrategia de anchura y la ubicación de una capa específica. El orden es en realidad determinado por las conexiones entre las capas, por lo que las estrategias regresan una lista ordenada de conexiones.
2. Calcula el valor de activación. Cada capa tiene una Calculadora de Conexión asociada, que toma su lista de conexiones (de la etapa anterior) y los valores de entrada (de otras capas) y calcula la activación resultante. Por ejemplo, en una simple red feedforward sigmoidal, la calculadora de conexión de la capa oculta toma los valores de las capas de entrada y sesgo (bias) (que son, respectivamente, los datos de entrada y una serie de 1s) y los pesos entre las unidades (en los casos de capas completamente conectadas, los pesos son, en realidad, almacenados en una conexión FullyConnected como un Matrix), calcula la suma ponderada, y alimenta el resultado a la función sigmoide. Las calculadoras de conexión implementan una variedad de transferencia (por ejemplo, suma ponderada, convolucional) y la funciones de (por ejemplo, logistic y tanh para perceptrón multicapa, binario para RMB) activación. La mayoría de ellos se pueden ejecutar en una GPU usando Aparapi y se puede usar con el entrenamiento mini-batch.

Computación GPU con Aparapi

Como mencioné anteriormente, una de las razones por las que las redes neuronales han hecho un resurgimiento en los últimos años, es que sus métodos de entrenamiento son muy propicios para el paralelismo, lo que le permite acelerar el entrenamiento de manera significativa, con el uso de un GPGPU. En este caso, decidí trabajar con la biblioteca Aparapi para añadir soporte GPU.

Aparapi impone algunas restricciones importantes sobre las calculadoras de conexión:

• Sólo se permiten matrices unidimensionales (y variables) de los tipos de datos primitivos.
• Sólo los miembros del método de la clase Aparapi Kernel, tienen permitido ser llamados desde el código ejecutable GPU.

Así, la mayoría de los datos (pesos, entrada, y las matrices de salida) se almacenan en las instancias Matrix, que utilizan matrices de flotador unidimensionales, internamente. Todas las calculadoras de conexión Aparapi utilizan ya sea AparapiWeightedSum (para capas completamente conectadas y funciones de entrada de suma ponderada), AparapiSubsampling2D (para capas de submuestreo), o AparapiConv2D (para capas convolucionales). Algunas de estas limitaciones se pueden superar con la introducción de la Arquitectura del Sistema heterogéneo (HSA). Aparapi también permite ejecutar el mismo código en ambos CPU y GPU.

Entrenamiento

El módulo de entrenamiento implementa diversos algoritmos de entrenamiento. Se basa en los dos módulos anteriores. Por ejemplo, BackPropagationTrainer (todos los entrenadores están utilizando el Trainer de la clase base) utiliza la calculadora capa feedforward para la fase feedforward y una calculadora especial de capa de anchura, para propagar el error y la actualización los pesos.

Mi último trabajo es el de apoyo de Java 8 y algunas otras mejoras, que están disponibles en esta rama y pronto se fusionaran con maestro.

Conclusión

El objetivo de este tutorial de aprendizaje profundo de Java era darle una breve introducción al campo de los algoritmos de aprendizaje profundo, comenzando con la unidad más básica de la composición (el perceptrón) y avanzando a través de diversas arquitecturas eficaces y populares, como la de máquina Boltzmann restringida.

Las ideas detrás de las redes neuronales han existido desde hace mucho tiempo; pero hoy en día, no se puede poner un pie en la comunidad de aprendizaje automático sin escuchar acerca de las redes profundas o alguna otra opinión sobre el aprendizaje profundo. La moda no se debe confundir con justificación, pero con los avances de la computación GPGPU y el impresionante progreso realizado por investigadores como Geoffrey Hinton, Yoshua Bengio, Yann LeCun y Andrew Ng, el campo sin duda muestra gran promesa. No hay mejor momento para familiarizarse e involucrarse como el actual.

FUENTE   toptal